前章では、「キャッシュフローの価値はその金額、タイミング、そして割引率によって決まる」という原理について解説しました。
ここでは、さらにこれを掘り下げ、より複雑なキャッシュフローはどのように計算するのか、実際の会社のバリュエーションはどの様にするのか、などについて見ていきます。また、DCF法の欠点や、それを補完する方法についても説明していきたいと思います。
複数の支払いがあるキャッシュフロー
前章では、未来の一時点において支払いが一度だけ発生するキャッシュフローの価値を計算する方法を解説しましたが、複数の支払いが発生するキャッシュフローについても同様にしてその価値を計算する事ができます。下のキャッシュフローを例にとって考えて見ましょう。

このキャッシュフローの価値はどの様に計算したらいいでしょうか。ちなみに、割引率は10%とします。
このキャッシュフローの現在価値は、1年目の100万円、2年目の百万円、そして3年目、4年目、5年目の百万円の現在価値の合計です。なので、キャッシュフロー全体の現在価値をPV、n年目のキャッシュフローの現在価値をPVnとすると、PVを求める式は以下の様になります。
PV = PV1 + PV2 + PV3 + PV4 + PV5
実際に計算して見ましょう。
まずは1年目の100万円について考えてみます。割引率は10%と仮定したので、1年後に受け取る100万円の現在価値は100万円を1.1で割った90.91万円となります。
おさらいを兼ねてなぜその様な計算方法になったのか確認すると、まず割引率が10%という事は、投資家がそれだけのリターンが見込めるのであれば投資をしても良い、と思っている事を表しています。そのため、この投資家にとって1年後の100万円と現在の90.91万円は等価だという様になります。
2年目の100万円についても同様に考えます。この投資家は自分の資金を年間10%の利回り、かつ複利で増やしていけるのならこのキャッシュフローへ投資してもいいと考えているので、2年目に受け取る100万円の現在価値は、それを1.21(1.1 x 1.1)で割ったものとなります。
同様の計算を3年目から5年目の100万円についても行うと、全ての年の100万円についてその現在価値を求める事ができます。計算の結果をまとめたのが下の表です。

各年の100万円の現在における価値を全て足し合わせると、キャッシュフロー全体の現在価値は次の様に計算できます。
キャッシュフローの現在価値 = 90.91 + 82.64 + 75.13 + 68.3 + 62.09 = 379.07(万円)
アニュイティ
次に、少し特殊なキャッシュフローについて考えて見ましょう。それはアニュイティと呼ばれるもので、毎年一定の金額の支払い(もしくは受け取り)が永久に発生するようなキャッシュフローです。
元々アニュイティとは、最初にまとまった保険金を支払うと永久に一定の額が支払われ続けるような保険商品のことで、転じて一定額が永久に発生し続けるキャッシュフローの事を指す様になりました。
後ほど説明しますが、アニュイティの計算式は驚くほどシンプルです。これを使うと、もしもこの会社が現在の利益を永久に稼ぎ続けるとしたらその価値はいくらか、といった感じで企業の価値をざっくりと見積もる事ができるので非常に便利です。
まずは例題を使って、公式を使わないアニュイティの価値の計算方法を見てみましょう。
例題:
ある会社が未来永劫にわたり年間1億円を稼ぎ続けるとしたら、そのキャッシュフローの価値はいくらになるでしょうか(※税金などは無視します)。割引率は10%とします。
答:
1億円のキャッシュフローが永久に発生しつづけるのなら、その価値は無限ではないかと思われるかもしれませんが、森の中の二羽の鳥より手元の一羽の方が価値があるという格言が示す通り、お金の価値も遠くなる程低下していきます。そのため、このキャッシュフローの現在価値は一定の値へと収束していくことになります。

高校数学で習う極限の知識を使ってこれを計算すると、その価値は10億円と求める事ができます。
アニュイティの公式
公式は複雑な計算過程を最も単純化したものですが、極限を使って計算するアニュイティの現在価値の計算も非常に簡潔な公式で表す事ができます。
アニュイティの現在価値を「PV」、毎年発生する支払いの額を「a」、割引率を「d」とおくと、これらの間には次の様な関係が成り立ちます。
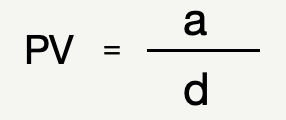
これは一定額の支払いが続く場合の公式ですが、一定の割合で支払額が成長していく場合に付いても非常に簡単な式で表す事ができます。キャッシュフローの成長率を「g」とすると、その式は以下の様になります。
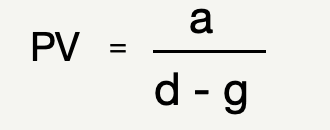
なお、この(d-g)をまとめて割引率と呼ぶ時もあります。
DCF法の使い方
ここまででDCF法の説明は終わりですが、これであらゆる会社のキャッシュフローの価値が正確に求められるかというと残念ながらそうはいきません。厳密に言えば、キャッシュフローの価値を求める事はできるのですが、「正確に」という点がネックになります。
トヨタ自動車のキャッシュフローの価値をDCF法で求める場合を例にとってどういう事か説明したいと思います。
まず、正確な推定を行うためには同社の未来永劫にわたるキャッシュフロー全てを正確に予測する必要がありますが、同社はグローバルにビジネスをしており、その業績は為替やマクロ経済をはじめ無数の事柄に影響されます。さらに自動車を取り巻く環境は技術面、社会面、環境面などの激しい変化に直面しているため、10年後や20年後はおろか、来年の業績でさえ正確に予測するのは経営者にとっても不可能に近いでしょう。
これがDCF法の一つ目の欠点です。キャッシュフローを正確に予測できれば正しい割引率を使う事でその正確な価値を求める事ができますが、そもそもそれ自体が相当に難易度の高い行為です。
そこで、精度の高い予測は諦めて、過去の利益の平均値から大まかな予測をしてみることにします。
同社の過去3年間の税引後利益は2.1兆円、2.3兆円、2.9兆円だったので、これらの平均値である2.4兆円が今後永久に続くものとしましょう。その場合、アニュイティの公式を用いればキャッシュフローの現在価値はわかります。では割引率は何を使ったらいいでしょうか。
前章で説明した通り、割引率の大きさには投資家が考えるリスクの大きさが反映されています。
そのため、ある投資家は「トヨタは歴史ある大企業であり安定しているので7%ほどの割引率が適当だ」と言うかもしれませんし、他の投資家は「EV、自動運転など自動車業界では大きな変化が起きている。トヨタの競争優位性は低下しているから12%の割引率が適当だ」言うかもしれません。さらに、「同社が成長しないのであれば9%ほどの割引率が適当だと思うが、今後は年率5%で成長していくので4%が適当だ」と考える投資家もいるかもしれません。
年間2.4兆円のアニュイティの価値は、7%の割引率を使えば34.3兆円(2.4兆円 ÷ 7%)ですが、12%であれば20兆円(2.4兆円 ÷ 12%)、4%であれば60兆円といった様に、用いる割引率によって大きく変化してしまいます。このような、割引率に対するセンシティビティの高さがDCF法のもう一つの欠点です。
DCF法の実践的な使い方
このように実践上の問題を抱えているDCF法ですが、理論的には完璧なので、何とかして使いたいものです。
上記の欠点のうち、キャッシュフローの予測の難しさに起因する問題については、予測が難しい会社を投資対象から外す事である程度回避できるでしょう。例えば事業を始めたばかりのテクノロジー企業、ヒット作の有無で大きく業績が左右されるゲーム企業や製薬開発企業、乱脈的なM&Aを繰り返す企業などはキャッシュフローの予測が極めて困難であるため、そもそもDCF法の概念を用いてキャッシュフローの価値を求める対象から除外してもいいと思います。
また、自分自身がインサイダーであるなどの理由から将来のキャッシュフロー予測に自信があったとしても、成長企業のバリュエーションにDCF法を使うのはリスクが高いでしょう。下の例を見てください。
架空の成長企業Aは研究開発やマーケットシェア拡大のために大きな成長投資を行っており、毎年1億円の赤字が出ています。水晶玉を通してこの会社の未来を覗いてみると、年間1億円の赤字は10年目まで続き、11年目に1億円の黒字を計上、そして12年目から20年目までは年間40%成長率は毎年40%、21年目から30年目までは20%、31年目から40年目までは10%、そして41年目以降はインフレ率と同じ2%の成長率で成長していく事がわかりました。この場合、各年におけるキャッシュフローの現在価値を表したグラフは下の様になります。なお割引率は10%としています。
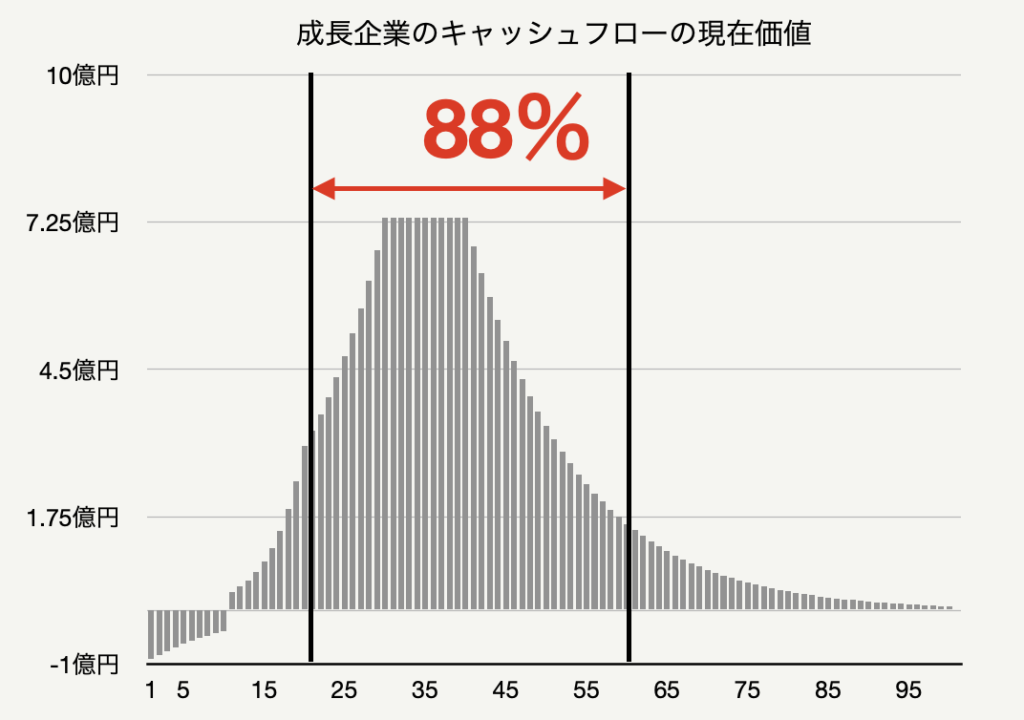
この成長企業Aの利益は未来へ行くほど大きくなるため、最初の20年間に発生するキャッシュフローの現在価値は総現在価値の3%に過ぎませんが、それとは対照的に、21年目から60年目までのキャッシュフローは総現在価値の88%にも及びます。
これがどういう事かというと、この成長企業Aのキャッシュフローの価値をある程度正確に求めるためには、60年先まで見通すビジョンが必要だと言う事です。より遠くの未来のキャッシュフローが現在価値に占めるウエイトが大きくなるため、成長企業のバリュエーションでは推定エラーが起きやすくなります。
これに対し、成長しない企業のバリュエーションはより近い未来のウエイトが大きくなります。
年間1億円の利益を今後永久に稼ぐ会社について、先ほどと同じ様なグラフを作ると、以下の様になります。
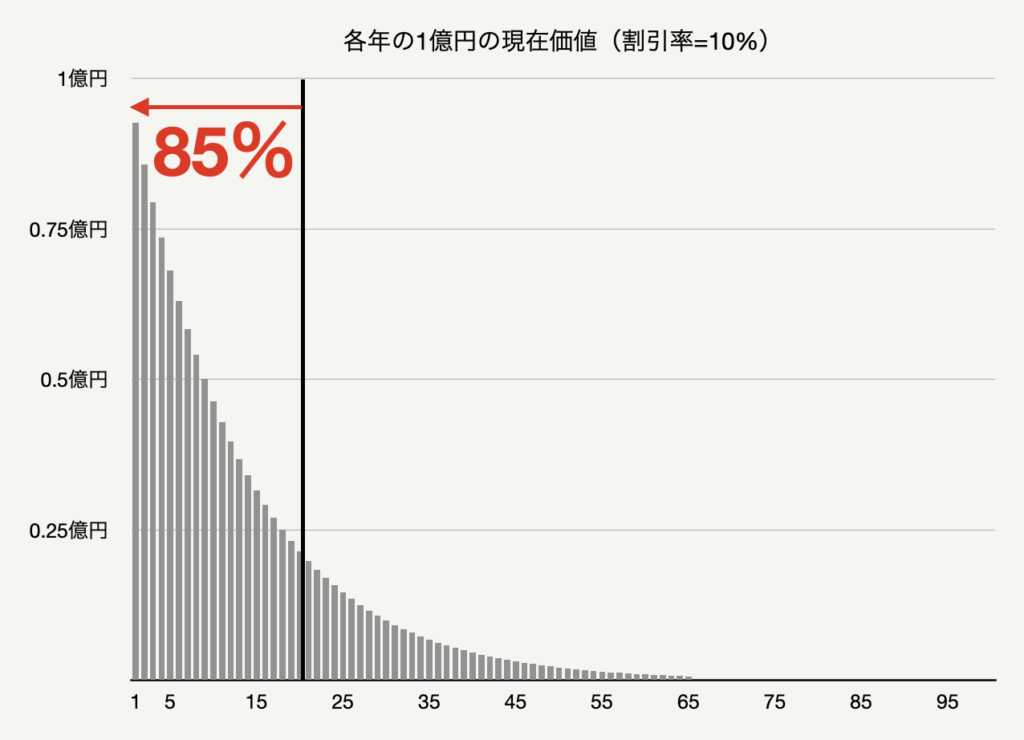
キャッシュフロー全体の現在価値のうち85%が今後20年のキャッシュフローによって占められています。
この事から、非成長企業のバリュエーションでは、遠い未来まで正確に予測する事の重要性は成長企業に比べて低くなり、よって発生する推定エラーは比較的小さなものとなります。
以上をまとめると、キャッシュフローの予測の難しさからくるDCF法の使いにくさは「予測の難しい会社を避ける」、「成長性の高い会社を避ける」といった方法である程度解決できそうです。
これらに当てはまらない会社については、点ではなくレンジ(範囲)でバリュエーションを行うことでキャッシュフロー予測のエラーを吸収する事ができます。
最も実現しそうなシナリオだけでなく、現実的な範囲で最も悲観的なシナリオに基づいたキャッシュフロー予測も行う事で、投資判断より保守的なものとすることができるでしょう。
次に、割引率に起因する問題の回避方法について見ていきましょう。
DCF法を用いる上でなぜ割引率が問題となるかというと、それは割引率の正解が投資家ごとに異なるからでした。
これを解決するためにまず考えられるのは、もっとも多くの投資家が合意しそうな割引率を推定する方法です。
ある会社について、予測キャッシュフローについては全ての投資家間で意見が一致していたとします。すると、その現在価値の推定結果は各投資家が用いる割引率の違いによってのみ変わってきます。
この様な場合、同社キャッシュフローの現在価値について前投資家の推定結果を集計すれば、その中央値は「最も多くの投資家が合意した割引率」を用いて計算した値になるでしょう。最も多くの投資家が合意しそうな割引率を使用するのが有効だと考えられるのはこの様な理由からです。
最も多くの投資家が合意しそうな割引率としては、以下の様なものがあります。
A)株式市場全体の割引率
B)対象企業が属する業界の割引率
C)対象企業の過去の割引率
A)株式市場全体の割引率
株式市場全体の割引率とは何かを説明する前に、まずは割引率と時価総額、そして利益の関係について理解する必要があるので解説したいと思います。
上で説明したアニュイティの概念を応用すると、会社の利益を適当な割引率で割ればそのキャッシュフローの価値がわかる事になります。ここで、このキャッシュフローの価値がその会社の価値、つまり時価総額であると単純化すれば、時価総額と現在の利益、そして割引率の間には次の様な関係が成り立ちます。
「時価総額 = 現在の利益 ÷ 適当な割引率」
これを変形させると、下の様に表す事ができます。
「適当な割引率 = 現在の利益 ÷ 時価総額」
PEレシオという言葉を聞いたことがある方もいるかも知れませんが、この式の右辺はその逆数となっています(Earnings ÷ Price)。
現在の利益と時価総額はどちらも調べればわかるので、これらを用いる事で投資家が使用した割引率を類推する事ができます。
これを株式市場全体に適用すれば、株式市場全体の投資家が使用している割引率が推定できます。※ここで言う割引率はアニュイティの公式にあるdではなく、投資家が期待する成長率も加味した(d – g)となります。
株式市場全体のPEレシオとしては、イエール大のロバート・シラー教授が考案したCAPEレシオという指標があります。CAPEレシオについての説明は割愛しますが、こちらのサイトのデータを参考にすると、NIKKEI225の過去5年ほどのCAPEレシオはおよそ18から20あたりで推移してきた事がわかります。
この逆数を取るとおよそ5%なので、過去5年間、NIKKEI225に含まれる企業へ投資する際に投資家が適用してきた割引率は平均して5%ほどであったと推測する事ができます。
この様に、株式市場全体(ここではNikkei225に含まれる225社)の割引率を使うのがまず一つ目の方法です。
しかし、実際は自分の投資しようとしている企業とNikkei225に含まれる企業の割引率が同じではない可能性もあります。
B)対象企業が属する業界の割引率
日本取引所が公開しているデータによると、2022年10月時点での主な業界のPEレシオ、及びその逆数として計算される割引率の推定値(PEレシオを基に著者が計算)は以下のようになっています。
| PEレシオ | 割引率(1 / PEレシオ) | |
| サービス業 | 20.3 | 4.9% |
| 建設業 | 10 | 10.0% |
| 機械 | 15.6 | 6.4% |
| 食料品 | 17.8 | 5.6% |
このように、PEレシオは業界によって比較的大きな違いがあることがわかります。
下の図は、主要なゼネコン5社と、スーパーマーケット5社のPEレシオの推移を示したグラフです。
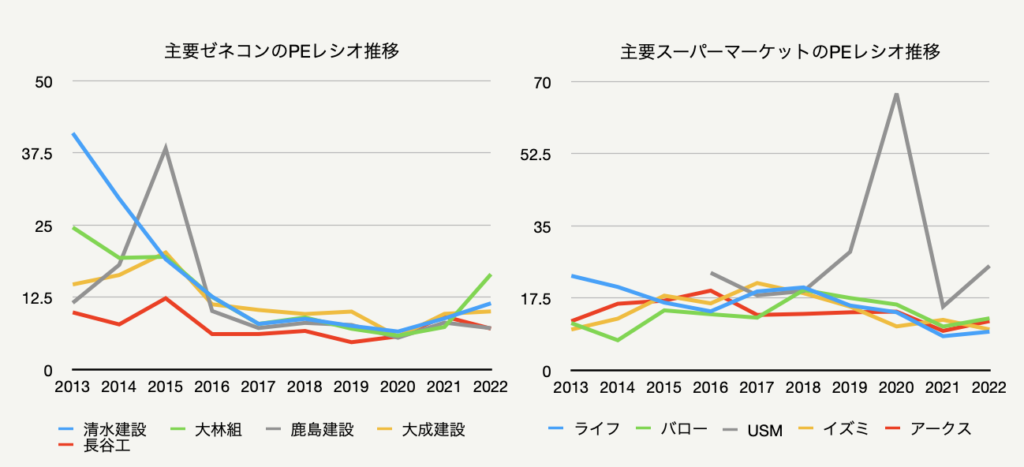
グラフから分かるように、同じ業界に属する企業のPEレシオは概ね同じようなレンジの中にあり、また数値の推移も似通っています。この事から、株式市場全体のPEレシオを使うよりも分析対象の企業が属する業界のPEレシオを用いた方がより正確な割引率の推定につながるでしょう。
C)対象企業の過去の割引率
適切な割引率を推定するもう一つの方法は、対象企業自体の過去のPEレシオを使う方法です。
同じ業界に属していても規模や運営効率、成長性などは会社ごとに異なります。そのため、対象企業自身の過去のPEレシオを参考にすれば、よりその会社に相応しい割引率を推定できるかも知れません。
ゼネコン主要5社それぞれについて過去10年のPEレシオを調べ、その中央値から各社の割引率の中央値を推定してみると以下の様な結果になりました。
| 清水建設 | 大林組 | 鹿島建設 | 大成建設 | 長谷工 |
| 9.8% | 9.3% | 12.3% | 9.8% | 14.5% |
ちなみに鹿島建設の2015年のPEレシオは38.27と他の年に比べて異常に高くなっていました。これを何かしらの原因による外れ値として除去すると、同社の割引率は12.3%ではなく9.9%と計算され、清水建設、大林組、大成建設とほぼ同じ様な値になります。長谷工だけは過去のPEレシオの中央値が6.9、推定割引率が14.5%とやや外れた値になっているので、何か同業他社とは異なるリスク要因がある可能性があります。
この様な場合、長谷工のバリュエーションについては業界全体の数字を使うよりも、長谷工自体の過去のPEレシオを参考にした数字を使う方が適切かも知れません。
割引率を使わない方法
ウォーレン・バフェットはバークシャー・ハザウェイの株主総会で「我々は公式な割引率といったものは持っていない」と発言したり、相棒のチャーリー・マンガーも「彼がDCF法を使っているところは見たことがない」と述べている事から、彼はDCF法を使わないで投資判断をしていると考えられている節があります。しかし、バフェットは「表計算ソフトを使った事はないが頭の中ではDCF法の計算を行っている」という趣旨の発言もしているので、これはやや現実とは異なった認識と言えます。
それでは、定まった割引率も使わず、かつ表計算ソフトも使わないで彼はどの様にDCF法を実践しているのでしょうか。
ヒントは次の発言の中にあります。
「我々は国債よりも高い利益を得られるものを買おうとしている。そこで問題なのはどれほど高いかだ。」
国債の利回りが3%の時、ある銘柄から期待できるリターンが5%であるとしたらこの銘柄は彼の投資基準の第一関門をパスできます。しかし、別な銘柄からは15%のリターンが期待できるとしたら、5%しか期待できないこの銘柄は躊躇なく捨てられるでしょう。
同様に、彼が25%のリターンを期待できる銘柄を見つければ、15%の期待リターンを持つ銘柄は捨てられます。
ここで大事なのは、彼がフォーカスしているのはより高い「利回り」を期待できる投資機会の発見であり、「正しい価値」の算定ではない、という点です。
DCF法はキャッシュフローの価値を計算するために使われる事が多く、そのため「現在価値 = ・・・」というように現在価値を主語として語られる事が多くなっています。
しかし、バフェットにとっての主語はあくまで「リターン」なので、彼はDCF法の式をリターンを主語としたものに変えているはずです。
どういう事なのか、例を使って見てみましょう。
仮に年間利益が1億円である会社があったとして、この会社のPEレシオが10倍だったとします。これを5年間保有した場合、期待リターンはどれほどになるでしょうか。なおここではバランスシートの価値は現時点においてゼロであるものとします。
1億円の利益に対してPEレシオは10倍なのでこの会社の現在の時価総額は10億円です。これは会社の生み出すキャッシュフローの価値について投資家が10億円の価値があると評価しているということでもあります。
この会社が5年後も同じく1億円を稼いでおり、かつ投資家の評価が変わっていないとすればその価値は10億円となるはずです。これに5年間で稼ぐ5億円のキャッシュの価値が加わるので、5年後の時価総額は15億円になっているはずです。
この会社の時価総額は5年で1.5倍となったので、もしも期間の始めに投資をしていれば50%のリターンが得られる事になります。5年間で50%の利益は年間リターンに直すと何%でしょうか。お金には複利で増えていく性質があるので、答えは8.5%です( 1.5^(1/6) = 8.5% )。
バフェットはこの様にして様々な投資機会の期待リターンを推定し、そしてそれらを比較する事でより高いリターンを得られる機会を常に探していると思われます。
この過程では割引率も求めていませんし、複雑な計算もしていません。しかしキャッシュフローの推定、複利、そして投資家によるキャッシュフローの値付け(割引率)といったDCF法の要素が全て盛り込まれています。
