バリュエーションとは、会社の価値を算定する行為です。
そして、会社の価値はバランスシートの価値とキャッシュフローの価値に分けられます。
バランスシートの価値とは保有する資産や負債から求められる価値で、例外はありますが、基本的にバランスシートを見ればそのおよその価値がわかります。
これに対し、キャッシュフローの価値は推測に基づいて求められるため、その額については人によって異なった意見となります。
具体的なキャッシュフローの価値の推定方法については次章以降で詳しく説明する事として、ここではまず、将来発生するキャッシュフローをどうやって現在の価値として表すのか、というところから解説していきたいと思います。
キャッシュフローの価値を計る物差し
身長や体重を測るとき、我々はそれらを国際的に決められたメートルやグラムと言った基準と比べますが、キャッシュフローにもその価値を測る基準となる指標が存在します。それは国債の利回りです。
まず国債とは何かというと、国がお金を調達するために発行する債券で、これを購入した人は事前に決められた利子を事前に決められた期日に受け取り、また満期には額面の払い戻しを受ける事ができます。
例えば10年満期、利子が年間1万円の国債を発行日に買ったとすると、この投資家は1年目から9年目までは毎年1万円の利子を受け取り、そして10年目には利子の1万円と額面の10万円を合わせた11万円を受け取る、と言うような感じです。
ではなぜこれがキャッシュフローの価値を測る基準になるのかと言うと、これが世の中のお金の増えるスピードを決定づけるからです。
次の説明を見てください。
ここに、一年後に満期を迎える額面100万円、利子3万円の国債があったとします。これを国債Aと呼ぶことにします。
国債Aを買った場合に受け取るキャッシュフローは以下の図のように表す事ができます。
<国債Aのキャッシュフロー>

今、国債Aの価格が100万円であったとします。すると、これを買うことで1年後には103万円のキャッシュを受け取る事ができるので、国債Aへ投資する事で得られるリターンは3%です。
国債は国が発行している債券であるため、事前に決められた利払いと額面の償還は「必ず」なされます。つまり、国債Aが100万円で買える世界というのは、3%のリターンは確実に実現できる世界ということになります。この様な無リスクで実現できる利回りのことを「無リスク利回り」と言います。
ここで、一年後に102万円を確実に受け取れる投資商品があったとします。そのような商品の値段は、3%のリターンが確実に実現できる世界では、100万円よりも高くなるでしょうか、低くなるでしょうか。
答えは国債Aを基準にすればわかります。一年後に102万円を確実に受け取る投資商品を100万円で購入した場合の利回りは2%と、国債Aの3%よりも低くなってしまいます。そのため、どちらも100万円であれば誰もが国債Aの方を買うでしょう。
この投資商品を売るためには値段を100万円よりも下げる必要が出てくるため、価格は100万円よりも安くなります。
また別な例を考えてみましょう。
今度は、1年後に105万円を確実に受け取れる投資商品です。これを100万円で買えばリスクを取ることなく5%の利回りを得る事ができるので、国債Aには誰も見向きもしなくなり、投資家はこの投資商品へ殺到することになります。
そうすると市場原理の働きにより、この投資商品の価格は100万円から競り上がっていきます。価格の上昇がどこで止まるかというと、利回りが3%になる金額です。なぜならばそれ以上高い値段で買えば利回りは3%を下回ることになり、投資家は国債Aを買った方がマシだとなるからです。
このように、国債の無リスク金利はその他のキャッシュフローの価格決定に影響を与えます。
金利が上がればキャッシュフローの価格は下がり、金利が下がればキャッシュフローの価値は上がる、といった様に、両者の間にはシーソーの様な関係があります(下図)。
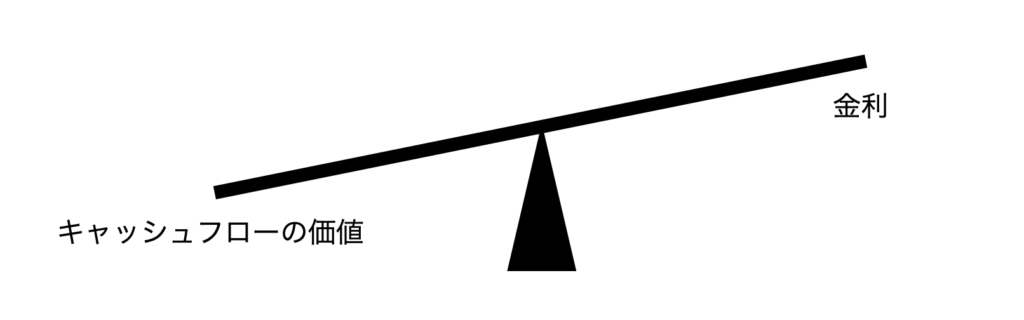
次にキャッシュフローの価値を具体的に計算する方法について見てみましょう。
ここに、今から2年後に一回だけ500万円のキャッシュフローが発生する無リスクの投資商品があったとします。国債Aの価格が100万円であるとき、この投資商品の価格はいくらでしょうか。
この投資商品のキャッシュフローは以下の様になります。

一年でお金が3%増える世界では、100万円の資金は二年間で106万円ではなく、106.09万円まで増加します。これは最初の一年間で得た3万円の利子に対しても二年目には3%の利子がつくためです。この様なお金の増え方を複利と言います。
二年間でお金を1.0609倍にできる世界では、今いくらあれば二年後に500万円まで増やすことができるでしょうか。答えは471万2979円です(500万円 ÷ 1.0609)。
これは、今471万2979円をもらうのと、二年後に500万円をもらうのは同じ価値であるということを表しています。言い換えると、無リスク利回りが3%の世界では、二年後の500万円の現在の価値は471万2979円であるという事です。
このようにして、未来のキャッシュフローは現在の価値に直すことができます。
無リスクでないキャッシュフロー
ここまでは、リスクのないキャッシュフローについて考えてきました。
しかし、企業の稼ぐ利益をはじめ、世の中のキャッシュフローのほとんどは予定されていたキャッシュフローの金額が変わるリスク、期待されたタイミングでキャッシュフローが発生しないリスクなど、何かしらのリスクが含まれています。
そこで、会社のキャッシュフローの価値を計算する際にはこのリスクに対して少し調整を加える必要があります。

まず原則を述べると、キャッシュフローに含まれるリスクが増加するほどそのキャッシュフローの価値は低下します。
例えば、二年後に500万円受け取るという先ほどの投資商品について、予定通り500万円支払われる確率が80%、300万円しか支払われない確率が20%であった場合、その価値は当然ながら、確実に500万円支払われる場合よりも低くなります。
仮に投資家が期待値の概念を使ったとすると、二年後に受け取るお金の期待値は460万円とな流(500万円 x 0.8 + 300万円 x 0.2 = 460万円)ので、このキャッシュフローの価値は471万2979円ではなく433.6万円(460万円 / 1.0609 = 433.6万円)となります。
全ての投資家がこの様に期待値で考える訳ではありませんが、少なくとも価値が471万2979円より低くなる事は確実です。
リスクプレミアム
仮に、上で見た二年後に80%の確率で500万円を受け取れる投資商品を433.6万円で買い、約束通り500万円の支払いを二年後に受けたとします。すると二年間での利回りは15.3%(500万円 ÷ 433.6万円)となり、一年あたりでは7.4%の利回りに相当します(
1.074 x 1.074 = 1.153)。
当然ながら、投資家はリスクの含まれたキャッシュフローへ投資するためにはより多くの見返りを要求しますが、この場合、それは無リスク金利の3%に対して上乗せされた4.4%によって表されています。この様に投資家がリスクを受容するために要求するプレミアムの金利を、リスクプレミアムと呼びます。
上の例ではキャッシュフローの発生するタイミングや金額、そして実現の確率がわかっていましたが、実際の株式投資においては企業の業績、株式市場の振る舞い、為替の変動など無数の要素がキャッシュフローに影響を与えるため、リスク要因はこれよりも遥かに多くなります。
リスク要素は多岐に渡りますが、代表的なものとしては以下の様なものがあります。
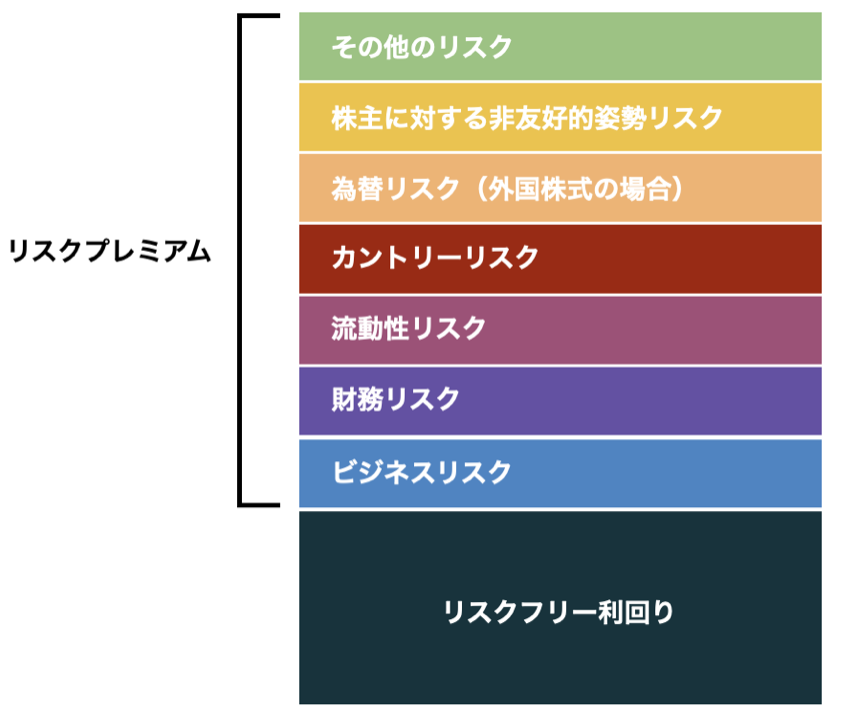
それではリスクプレミアムはどの様に計算するかというと、誰もが納得するようなただ一つの計算方法はありません。
ある人はCapital Asset Pricing Model (CAPM)という金融工学の手法を使ったり、ある人は10年国債利回りプラス6%を使ったり、またある人は一律10%を使ったりとさまざまな方法でリスクプレミアムを「探って」います。
無リスク利回りにリスクプレミアムを足したものをまとめて割引率と言いますが、以上の様な理由から、キャッシュフローを現在の価値に直す際に使用する割引率は投資家ごとに事なったものとなります。
割引率を求める基準が一つでないならば、同じキャッシュフローでもその現在価値は一つに定まらないではないか、と思われたもしれませんが、まさにその通りで、次の章で解説するDCF法(Discounted Cash Flow)によるキャッシュフローの価値算定はそれを実行する人によって時に大きく異なる値になる事があります。
ともあれ、現時点では「キャッシュフローの価値はその金額、タイミング、そして割引率によって決まる」という原則を覚えておけば大丈夫です。
キャッシュフローの価値、キャッシュフローのタイミング、キャッシュフローの金額、そして割引率の間には、以下の式で表される様な関係があります。これは、投資においては物理学にとっての熱力学第二法則くらい重要なもので、あらゆるキャッシュフローの現在価値はこれを応用することで計算されます。
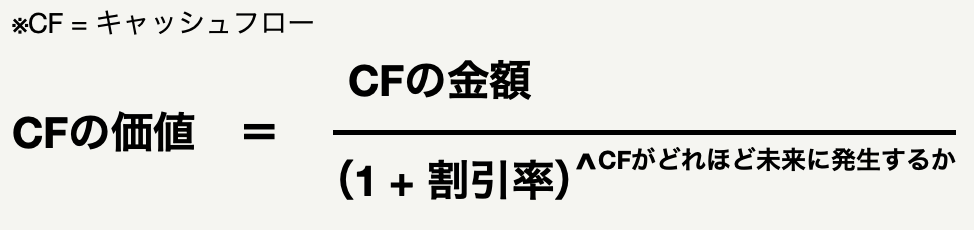
次章では、このコンセプトをベースとして、より具体的なキャッシュフローの価値の求め方について解説していきたいと思います。
